Einführung in die Auswertung
Mit dem Aufbau sind Datensätze von Myonenzerfällen aufgenommen und gespeichert worden. Für die Auswertung sind folgende Schritte notwendig:
- du schaust dir vom Oszilloskop gespeicherte Bilder an, in denen die Signale vom Myon und vom Elektron zu sehen sind.
- für jedes Bild bestimmst du die Zeitdifferenz zwischen dem Myonsignal und dem Signal vom Elektron.
- du fasst die Zeitdifferenzen auf einer Strichliste zusammen.
- aus der Strichliste fertigst du mit einem Tabellenkalkulationsprogramm eine Graphik an.
- als Nächstes passt du in der Graphik eine exponentielle Trendlinie an, um die mittlere Lebensdauer des Myons zu bestimmen.
Im Folgenden wird die Auswertung Schritt für Schritt begleitet.
Als Erstes muss geklärt werden, wie der Myonenzerfall am Oszilloskop aussieht, damit er auch erkannt werden kann.
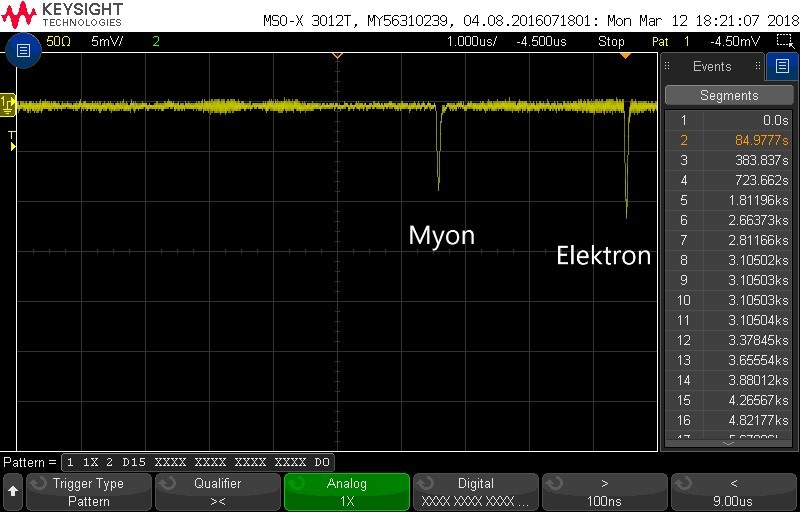
Beim Myonzerfall haben die vom Oszilloskop gespeicherten Bilder die Gemeinsamkeit, dass immer zwei Signale (Pulse) zu sehen sind und der rechte, also der zweite Puls immer in der Mitte der zehnten Spalte des Bildschirms positioniert ist.
Der erste Puls entsteht, wenn das Myon in das Wasser eindringt und Cherenkov-Strahlung erzeugt. Der Zweite entsteht, wenn das Myon zerfällt und das Zerfallsprodukt auch Cherenkov-Strahlung erzeugt. Wenn beide Pulse niedriger als -4 mV (die sogenannte Triggerschwelle) sind, zeigt das Oszilloskop einen sogenannten Doppelpuls. In diesem Fall wird das Bild des Doppelpulses gespeichert. Die maximal ablesbare Zeitdifferenz ist 9,5 µs.
Innerhalb von 9,5 µs kann es passieren, dass zwei Myonen Cherenkov-Strahlung erzeugen und so einen Doppelpuls erzeugen - dies nennt man zufällige Koinzidenz. Diese Doppelpulse können nicht von Myonenzerfällen unterschieden werden.
Bilder, die wir für die Auswertung nicht verwenden können, werden durch elektronisches Rauschen oder andere Störungen (zum Beispiel im Stromnetz) hervorgerufen. Diese werden als Schrott bezeichnet.
Um die Doppelpulse sortieren zu können, ordnet man sie verschiedenen sogenannten Bins (englisch für Klassen) zu.
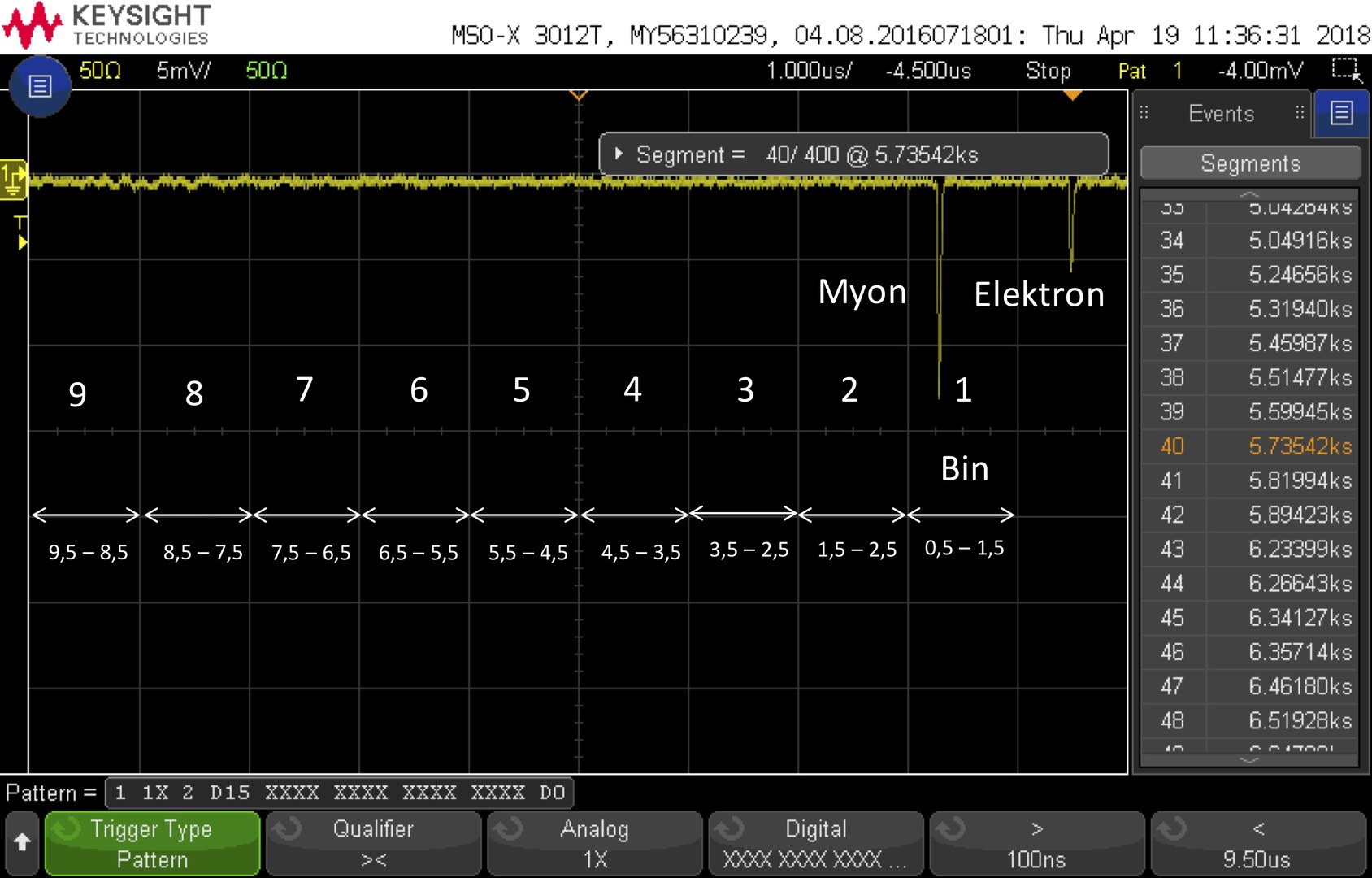
Der Zeitraum von 0 µs bis 0,5 µs wird nicht für die Auswertung betrachtet, da das Oszilloskop einen gewissen zeitlichen Abstand benötigt, um zwei Signale voneinander trennen zu können.
Durch die feste Positionierung des zweiten Pulses ist das Ablesen des Zeitfensters, in dem der erste Puls stattfand, einfacher. Im gezeigten Fall liegt der Myonpuls im 1. Bin also innerhalb von 0,5 µs bis 1,5 µs vor dem Elektronenpuls.
Die Nummerierung der Bins ist nicht auf den Bildern ersichtlich. Für die Auswertung ist es also hilfreich, eine DIN A4 Schablone quer vor den Monitor zu legen.
Die Bilder sind in Paketen zusammengefasst, die jeweils ca. 400 Bilder enthalten. Damit die statistische Grundlage größer wird, sollten möglichst viele verschiedene Datenpakete ausgewertet werden. Diese Datenpakete findest du auf der Downloadseite.

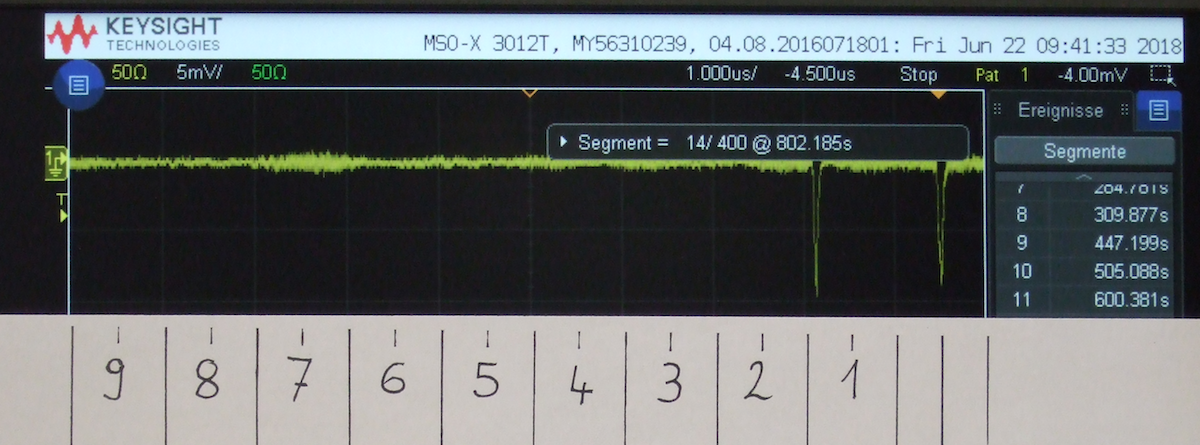
Die Auswertung läuft besonders gut, wenn zwei Personen zusammenarbeiten. Eine interpretiert die Bilder, die Andere führt eine Strichliste. Diese Strichliste kann per Hand erstellt oder ausgedruckt werden. Die Strichliste findest du auch auf der Downloadseite.
Hier siehst du ein Beispiel für eine ausgefüllte Strichliste. Mit Schrott werden die Bilder bezeichnet, die nicht nutzbar sind, also zum Beispiel Störungen oder drei Pulse auf einem Bild.
Die Summen aus den Strichlisten werden dann in ein Tabellenkalkulationsprogramm übertragen und dort in eine Streupunkte-Grafik übersetzt. Vorbereitete Auswertedateien findest du auch auf der Downloadseite.
Wenn die Daten aus der Strichliste im Tabellenkalkulationsprogramm eingegeben wurden, kann die exponentielle Trendlinie angepasst und die Kurvengleichung angezeigt werden.
In dieser Kurvengleichung kann im Exponenten die Zerfallskonstante abgelesen werden. Der Kehrwert der Zerfallskonstanten ist die mittlere Lebensdauer. Die Messdauer (Zeit) kann dem letzten Doppelpulsbild in der Spalte Segmente entnommen werden.
Die Trendkurve strebt für große Zeiten gegen Null. In den Daten gibt es Zufallskoinzidenzen, die gleichverteilt sind und einen sogenanten Untergrund oder Offset bilden. Daher beschreibt die Trendkurve die experimentellen Daten nicht optimal. Da die Tabellenkalkulationsprogramme diesen Untergrund nicht berechnen können, muss der Offset hier per Hand eingestellt werden.
Wenn die Daten der Kleingruppen zusammengefasst werden, ergibt sich ein genaueres Bild, da sich die statistischen Schwankungen gegenseitig ausgleichen.
Vorbereitete Auswertedateien findest du auch auf der Downloadseite.
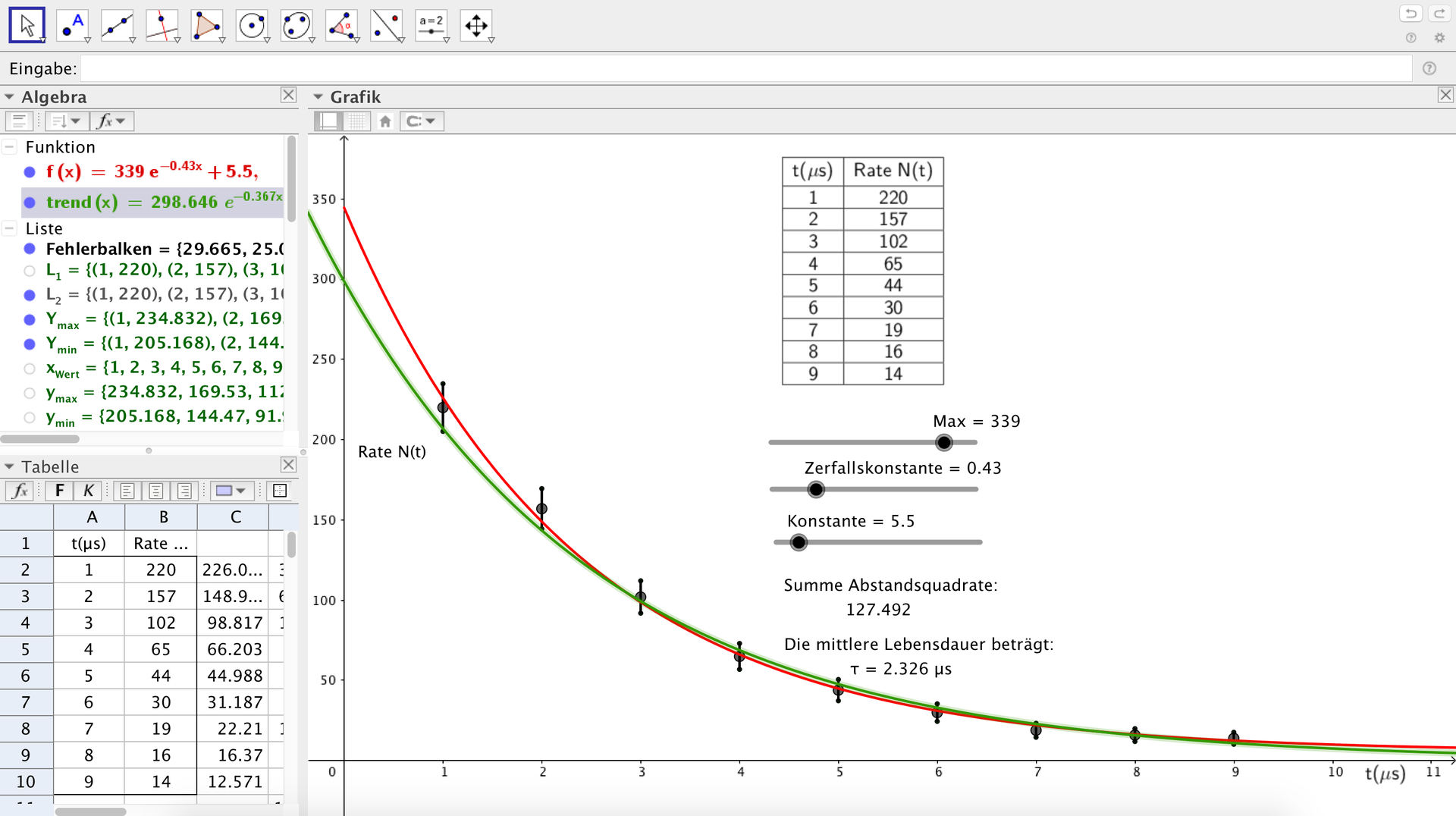
In GeoGebra können, wie in Tabellenkalkulationssystemen, Tabellen in Grafiken umwandeln und Trendlinien einfügt werden. Darüber hinaus kann man mit Geogebra eigene Funktionen definieren, die eine verbesserte Anpassung ermöglichen.
Als Startwerte verwendet man die Werte aus der Trendfunktion (grün) und optimiert die verbesserte Anpassung (rot), indem die Summe der Abstandsquadrate minimiert wird.
Wenn die bereitgestellte Datei verwendet wird, müssen nur die Werte in die Tabelle unter Rate N(t) eingefügt werden, bevor die Optimierung angegangen werden kann.
Eine vorbereitete Auswertedatei findest du auch auf der Downloadseite.
Dies hängt mit den verwendeten Einstellungen am Oszilloskop zusammen.
Der erste Puls schaltet scharf und der zweite löst das Speichern der Messwerte 9,5 µs vor dem Auslösen bis 0,5 µs nachher aus. Der Abstand der beiden Pulse ist abhängig von dem einzelnen Zerfall und damit ist der linke Puls nicht immer an der gleichen Stelle.
Zufallskoinzidenzen können auch mit Zerfallsereignissen vorkommen.
Dann sind manchmal drei Pulse auf den Bildern und es ist nicht zu erkennen, welcher Puls nicht zum Zerfall gehört. Daher wird dieses Bild nicht als Doppelpuls gezählt. Das gleiche gilt für Bilder, auf denen viel Rauschen zu sehen ist.
Wenn zwei Myonen Cherenkov-Strahlung im Behälter erzeugen, nennt man dies zufällige Koinzidenz.
Diese Doppelpulse können nicht von Myonenzerfällen unterschieden werden. Die Zeitdifferenzen zwischen den Pulsen sind aber in diesem Fall nicht exponentiell sondern gleichverteilt. Dies erzeugt den Offset.
Das lässt sich nicht vorhersagen, lediglich Durchschnittswerte für große Anzahlen von Myonen sind bestimmbar.
Dazu kommt bei der Höhenstrahlung die Schwierigkeit, dass wir den Zeitpunkt der Entstehung eines einzelnen Myons nicht bestimmen können. Im Schülerversuch werden wir uns damit beschäftigen, die mittlere Lebensdauer der Myonen zu bestimmen.